引言
区块链技术作为一种去中心化的分布式账本技术,正迅速改变金融、供应链管理、智能合约等多个领域。在区块链的核心,安全性是至关重要的,而加密技术是确保这种安全性的基础。本文将探讨区块链中的主要加密技术,包括哈希函数、数字签名、对称加密和非对称加密,并介绍一些进阶加密技术,如零知识证明和同态加密。
常见的数据加密类型
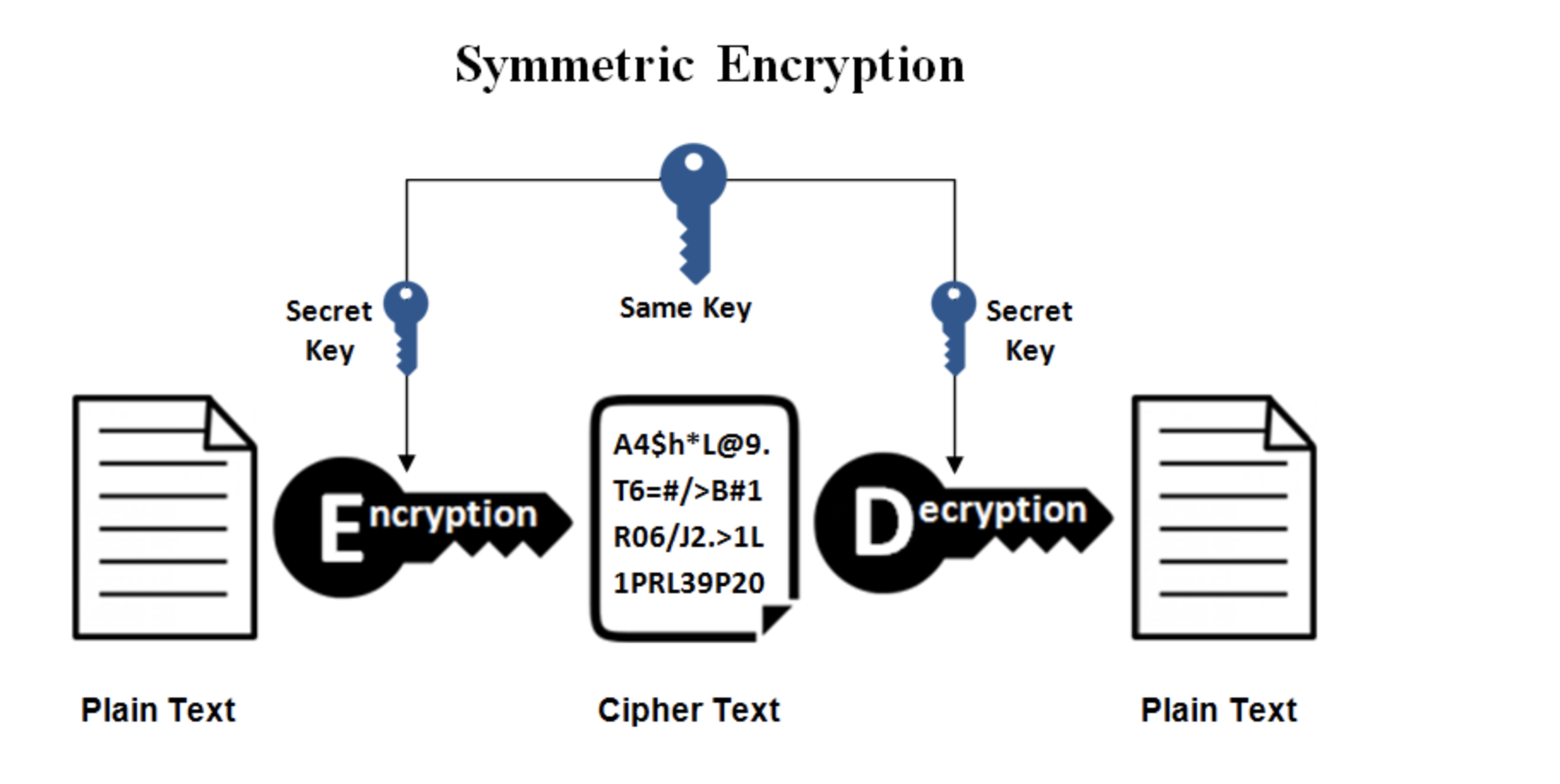
对称加密
- 工作原理:对称加密使用相同的密钥来加密和解密数据。这意味着发送方和接收方必须事先共享密钥。加密和解密的过程都使用同一个密钥,因此速度很快。
- 使用技术:常见的对称加密算法包括DES(数据加密标准)、3DES、AES(高级加密标准)等。
- 应用场景:对称加密适用于需要高效加密和解密大量数据的场景,比如数据存储、数据传输等。但是由于密钥需要提前共享,安全性依赖于密钥的保护和分发,因此不适用于公开通信环境。
非对称加密:
- 工作原理:非对称加密使用一对密钥(key pair) ,分别称为公钥和私钥。公钥用于加密数据,私钥用于解密数据。这意味着发送方可以使用接收方的公钥加密数据,只有接收方持有相应的私钥才能解密数据。
- 使用技术:常见的非对称加密算法包括RSA、DSA、ECC等。
- 应用场景:非对称加密适用于安全通信场景,特别是在网络传输中,如SSL/TLS协议中的证书交换,数字签名等。它提供了更好的安全性,因为私钥不需要传输或共享,而且即使公钥泄露也不会影响数据的安全性。

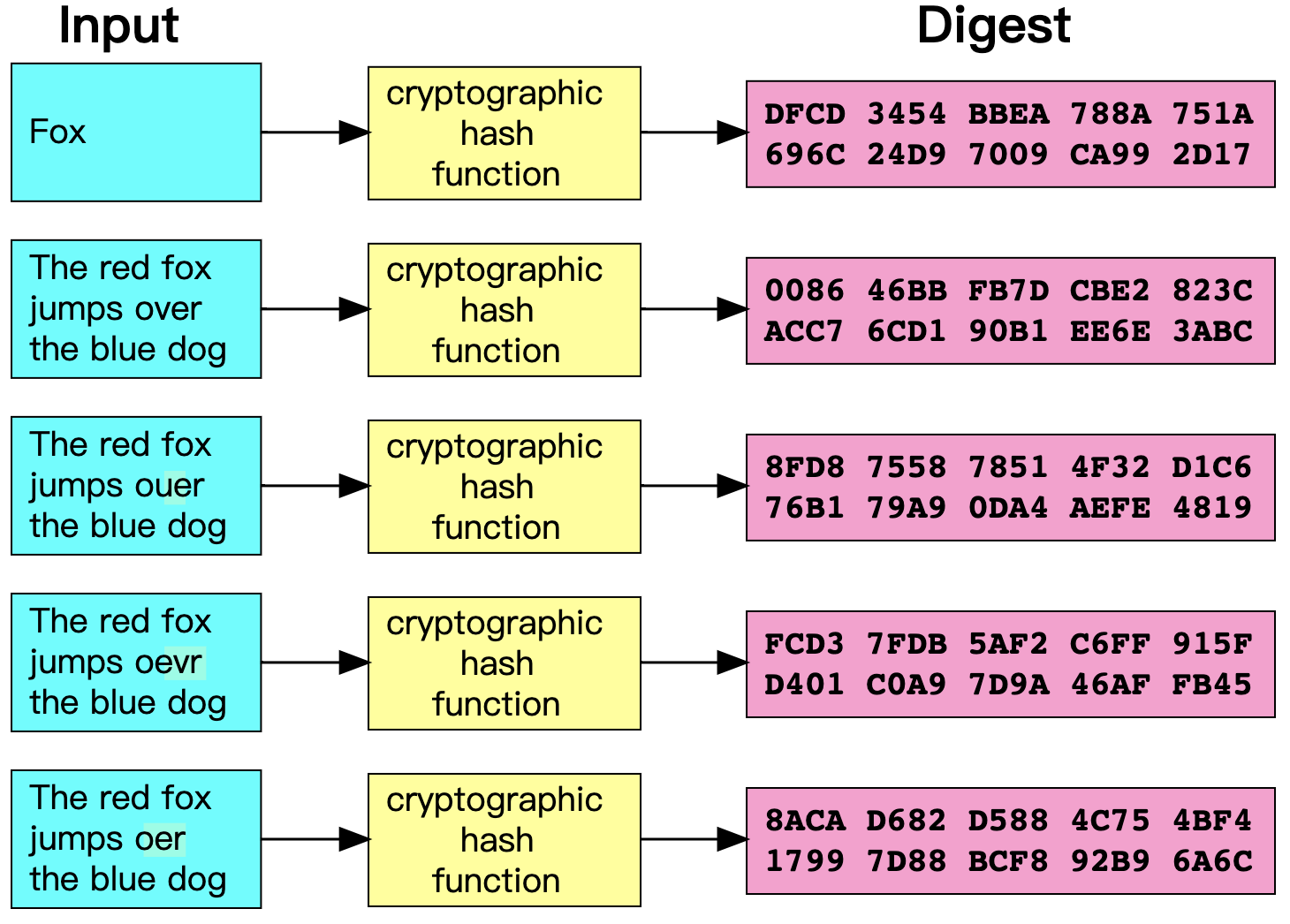
哈希加密(Cryptographic hash function) :
- 工作原理:哈希加密是将输入数据转换为固定长度的哈希值,无法从哈希值还原出原始数据。
- 使用技术:常见的哈希函数包括MD5(目前被认为不安全,容易被破解)、SHA等
- 应用场景:它的主要应用场景包括数据完整性验证、文件完整性验证、密码散列存储和数字签名
区块链中的加密算法
对称加密在区块链中主要用于数据保护和加密通信,但其密钥管理复杂且不提供身份验证,这限制了其在区块链核心机制中的应用。相比之下,椭圆曲线密码学(ECC)作为一种非对称加密技术,提供高安全性和计算效率,广泛用于生成数字签名和安全密钥交换,成为区块链中关键的加密解决方案。
椭圆曲线加密
椭圆曲线加密(Elliptic Curve Cryptography,ECC)是一种公钥密码学系统(public key cryptographic system),这种系统有一个特点是在一个方向上易于处理,但是在相反方向计算是非常困难的,这个在算法上叫Trap door Functions.
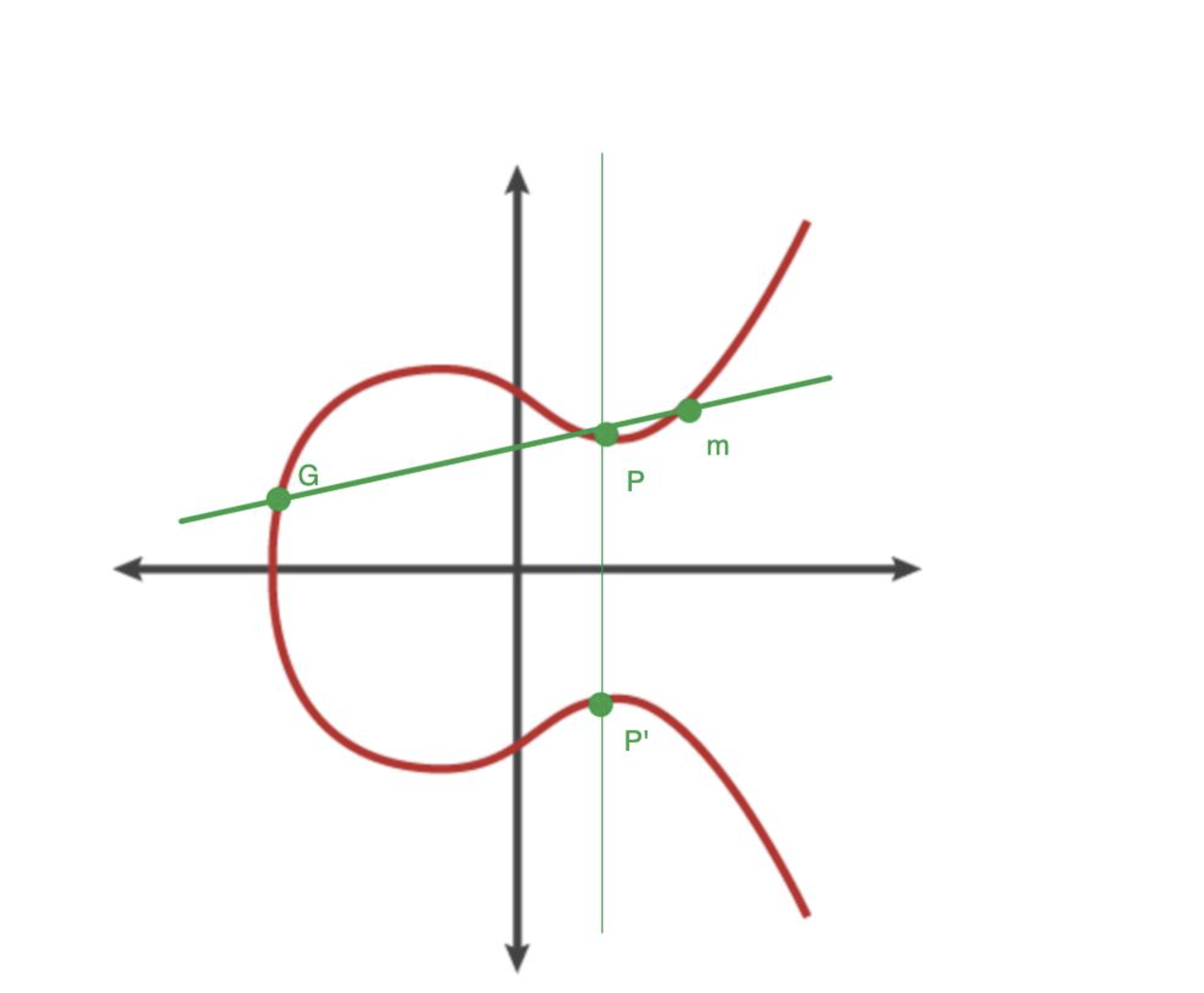
椭圆曲线基本特性是:
- 需要满足公式:y2 = x3 + ax + b,
- 关于x轴对称(如图:p ,p’)
- 任意非垂直线与曲线的交点最多为三个(如图:G,P,m)
- 曲线上的任意两点可以相乘得到一个新的点(G dot P = m)
以下是椭圆曲线加密的一般步骤和应用:
在椭圆曲线加密中,私钥是不需要通过任何计算得来的,而是随机选择的一个数。私钥通常是一个很大的数,而这个数是secret,只有私钥的持有者知道。
公钥的生成是基于私钥的:首先,选择一个公共基点(public point),记为 G;然后,将你的私钥 priv 作为一个标量,与基点 G 进行点乘操作,即 G 与自己相加 priv 次。标量点乘的结果是另一个曲线上的点,这个点就作为公钥,我们记为 P(公钥 P = 私钥 priv × 基点 G, 这里的 × 表示椭圆曲线上的标量乘法操作,而不是传统意义上的乘法或幂运算(^)。椭圆曲线上的点加法和标量乘法都是特殊定义的,与传统的算术运算规则不同)。从公钥计算得到私钥的这个过程在椭圆曲线密码学中被称为椭圆曲线离散对数函数(elliptic curve discrete logarithm function)。在数学上,这是一个难解的问题,尤其是当素数很大时。这个性质成为了我们所寻找的阱门函数(Trapdoor Function),这正是公钥加密和数字签名系统所依赖的基础,也是加密算法安全性的关键。
椭圆曲线在区块链中的应用:
1. 公钥-私钥
生成椭圆曲线算法用于生成公钥和私钥对,这对区块链用户至关重要。公钥用于生成钱包地址,而私钥则用于签署交易,控制资金和验证身份。
- 公钥生成: 从私钥生成公钥是一个数学运算,涉及椭圆曲线上的点乘。
- 私钥保护: 私钥必须安全保管,因为拥有私钥即拥有账户中的所有资产。
以下是比特币、以太坊和 Solana 如何利用公钥来实现钱包地址:
- 比特币:使用 secp256k1 椭圆曲线算法,地址生成包括 SHA-256 和 RIPEMD-160 哈希处理、Base58 编码等步骤。地址以 1、3 或 bc1 开头。
- 以太坊:使用 secp256k1 椭圆曲线算法,地址生成包括 Keccak-256 哈希处理。地址以 0x 开头。
- solana:使用 Ed25519 椭圆曲线算法,地址直接使用公钥的 Base58 编码表示。没有额外的哈希处理步骤。地址为 44 字节的 Base58 编码字符串。
2. 数字签名椭圆曲线数字签名算法用于签署交易。签名过程确保交易的完整性和来源的合法性,不可篡改性。
- 签署交易: 用户用私钥对交易数据进行签名,创建数字签名。
- 验证签名: 其他节点使用公钥验证签名的有效性,确保交易未被篡改且确实由持有相应私钥的人发起。有三个主要目的。首先,签名证明了私钥的控制者,即资金的所有者,已经授权支出这些资金。其次,授权的证明是不可否认的(不可抵赖性)。第三,被授权的交易无法被未经认证的第三方更改——这确保了交易的完整性。在以太坊和Solana中,交易还包括对智能合约的调用,这也需要数字签名来确认调用的合法性。
3. 身份验证椭圆曲线算法用于身份验证,确保只有授权用户能够访问特定的区块链资源或进行某些操作。
- 用户身份: 通过数字签名和公钥验证用户身份。
- 智能合约: 在智能合约中使用数字签名来验证合约调用者的身份。
4. 多重签名
多重签名是指在进行交易或执行操作时,需要多个签名才能完成操作。这个机制可以显著提高账户的安全性和控制力,特别是在区块链和加密货币中。多签通常由椭圆曲线算法支持,通过生成多个密钥对和对应的签名来实现。这种机制对于企业账户、大额资金管理以及去中心化治理等场景都非常重要。
哈希加密
哈希函数的主要特征包括:
- 确定性(Determinism): 给定一个输入消息,总是生成相同的哈希输出。
- 可验证性(Verifiability): 计算消息的哈希值是高效的(线性复杂度)。
- 非相关性(Noncorrelation):对消息做一个很小的改变(例如改变1比特),应该使得哈希输出发生广泛的变化,以至于无法将其与原始消息的哈希值相关联。
- 不可逆性(Irreversibility):从哈希值计算出原始消息是不可行的,相当于通过所有可能的消息进行暴力搜索。
- 碰撞保护(Collision Protection):计算出两个不同的消息产生相同的哈希输出应该是不可行的。在区块链技术中,哈希函数同样扮演着重要的角色,且不同的区块链往往采用不同的哈希算法来满足特定的安全和性能需求。
以下是一些主流区块链及其采用的哈希算法。
比特币 (Bitcoin)
- 主哈希算法:SHA-256(Secure Hash Algorithm 256-bit)
- 用途:挖矿过程(工作量证明,Proof of Work)、交易哈希、区块哈希、Merkle树
以太坊 (Ethereum)
- 主哈希算法:Keccak-256(常误称为SHA-3)
- 用途:交易哈希、地址生成、智能合约数据校验、Merkle树
Solana
- 主哈希算法: SHA-256 和 SHA-3
- 1用途:
- SHA-256: 主要用于PoH(历史证明)、数据校验、生成唯一标识符
- SHA-3: 用于智能合约执行和数据校验## 结语区块链加密技术为数字资产的安全提供了坚实的保障。通过非对称加密技术和先进的加密算法,用户可以在区块链上进行安全的交易和通信,确保数字资产的保值和流通。